Circumscris triunghiului echilateral, triunghiuri

Circumscris triunghiului echilateral, posedă toate proprietățile descrise triunghi arbitrar în jurul circumferinței și, în plus, are propriile sale proprietăți.

1) Centrul cercului circumscris triunghiului - punctul de intersecție a midperpendiculars laturile sale.

Deoarece mediana, altitudinea și bisectoare coincid într-un triunghi echilateral. să fie centrul unui triunghi echilateral în jurul cercului se află la intersecția sale mediane, altitudini și Bisectors.

De exemplu, în triunghiul dreptunghic ABC AB = BC = AC = o

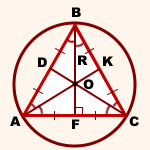
Punctul O - circumscris.

AK, BF și CD - mediana, altitudinea și bisectoarea triunghiului ABC.

2) Distanța dintre centrul cercului circumscris vârfurile triunghiului este egală cu raza. După cum este descris cu privire la centrul unui cerc triunghi echilateral se află la intersecția dintre medianele sale și mediana triunghiului la punctul de intersecție sunt divizate într-un raport de 2: 1. numărând de sus, raza cercului circumscris este de două treimi din lungimea medianei:

Astfel, formula de cerc cu raza descrisă despre triunghiul echilateral -

In schimb, o parte triunghi echilateral cu raza cercului circumscris -

3) Formula pentru a găsi zona unui triunghi echilateral pe partea sa -

Prin urmare, putem găsi zona razei cercului circumscris:

Astfel, formula zona pătrată a unui triunghi regulat al raza cercului circumscris -

4) Gym descris triunghi aproximativ dreapta coincide cu centrul cercului cercului inscris acolo.

5) Raza cercului descris de aproximativ un triunghi echilateral, este de două ori raza cercului inscris: