Cum de a calcula viteza instantanee

anterior ◈ următoarea

Viteza - este viteza de deplasare a obiectului în direcția dorită. [1] Pentru a găsi viteza obiectului comun (v) - deplasarea (e) o sarcină simplă să fie împărțită pentru un timp (e) predeterminată la acest moment (t), adică de a folosi formula v = s / t. Cu toate acestea, o astfel de metodă, viteza medie a corpului. Folosind unele din calcule pot fi găsite viteza a corpului, în orice punct pe cale. Această viteză se numește viteza instantanee și se calculează cu formula: v = (ds) / (dt). adică reprezintă un derivat de formula pentru a calcula viteza medie a corpului. [2].

pași Editare

Partea 1 din 3: Se calculează viteza instantanee Editare

Pentru a calcula viteza instantanee este necesară cunoașterea ecuația care descrie deplasarea corpului (poziția ei la un moment dat), adică, o astfel de ecuație, dintre care o parte este s (mișcarea corpului), iar pe de altă parte - membrii ai t variabila (timp). De exemplu:

s = -1.5t 2 + 10t + 4

În această ecuație: Muta = s. Mutarea - obiect a trecut drumul. De exemplu, în cazul în care organismul este mutat la 10 m în fața și în spatele de 7 m, corpul total de deplasare 10 - 7 = 3 m (un 7 + 10 = 17 m). Timpul = t. De obicei, măsurată în secunde.

Pentru a găsi viteza instantanee a unui corp ale cărui mișcări sunt descrise de ecuația de mai sus, trebuie să se calculeze derivata acestei ecuații. Derivata - această ecuație ne permite să calculeze panta în orice punct (în orice moment). Pentru a găsi derivatul, Diferentierea funcția după cum urmează: în cazul în care y = a * x n. derivatul = a * n * x n-1. Această regulă se aplică fiecărui membru al polinomului.

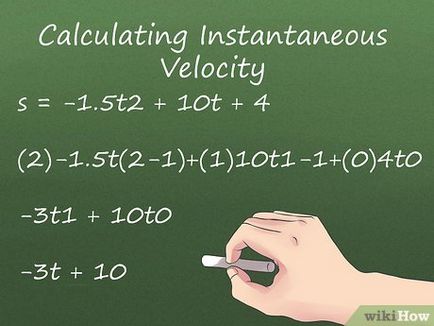
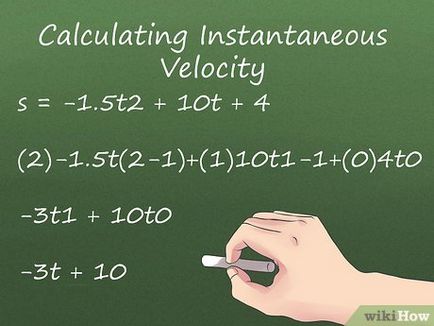
Cu alte cuvinte, fiecare membru al derivatului cu privire la t este egal cu produsul de multiplicare (în picioare în fața unei variabile) și gradul variabilei înmulțit cu variabila în măsură egală cu minus puterea inițială 1. Termenul constant (termenul fără o variabilă, adică numărul) dispare deoarece este multiplicat cu 0. În acest exemplu:

s = -1.5t 2 + 10t + 4
(2) -1.5t (2-1) + (1) 10t 1 - 1 + (0) 4t 0
-3t 1 0 + 10t
-3t + 10

Înlocuiți „s“ on „ds / dt“, pentru a arăta că noua ecuație - un derivat al ecuației inițiale (adică, derivata s t). Derivatele - este panta graficului la un anumit punct (la un moment dat). De exemplu, pentru a găsi panta liniei descrisă de o funcție s = -1.5t 2 + 10t + 4 la t = 5, pur și simplu înlocuirea în ecuația 5 derivat.

În acest exemplu, ecuația ar trebui să fie derivat după cum urmează:

În derivatul ecuație substituie valoarea corespunzătoare t, pentru a găsi viteza instantanee la un moment dat. De exemplu, dacă doriți să găsiți viteza instantanee la t = 5, pur și simplu înlocui 5 (în loc t) în ecuația ds derivate / dt = -3 + 10. Apoi decide cu ecuația:

ds / dt = -3t + 10
ds / dt = -3 (5) + 10
ds / dt = -15 + 10 = -5 m / s

Acordați atenție la unitatea de măsură a vitezei instantanee: m / s. Din moment ce sunt date valoarea deplasării în metri și în timp - în secunde, iar viteza este raportul de mișcare a timpului, unitatea de măsură m / s - este corect.

Partea a 2 din 3: Evaluarea grafică a vitezei instantanee Editare

Graficul de mișcare a corpului. În capitolul anterior, ați calculat viteza instantanee a formulei (derivatul ecuație permite să găsiți pantei la un anumit punct). Prin reprezentarea grafică mișcarea corpului, puteți găsi panta în orice punct, și, astfel, determină viteza instantanee la un moment dat.

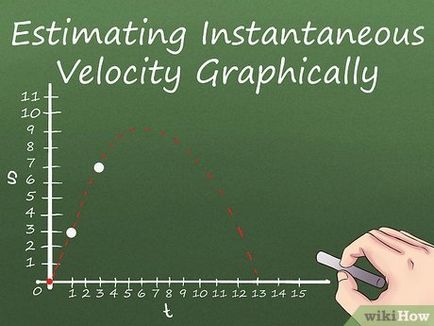
Axa Y întârziere deplasare, iar axa X - timp. Coordonatele punctelor (x, y) primesc prin substituirea diferitelor valori ale lui t în ecuația originală și calcularea valorilor de deplasare corespunzătoare s.
Graficul poate cădea sub axa X. Dacă corpul graficului de deplasare este sub axa X, atunci acest lucru înseamnă că organismul se mișcă în direcția opusă din punctul de pornire al mișcării. De regulă, programul nu se va aplica pentru axa Y (valori negative ale lui x) - nu măsurați viteza obiectelor în mișcare înapoi în timp!

Selectați graficul (curba) și punctul P este aproape de ea punctul Q. Pentru a găsi panta graficului de la punctul P, vom folosi conceptul de limită. Întindere - o stare în care valoarea secantă tras prin două puncte P și Q, situată pe curba se apropie de zero.

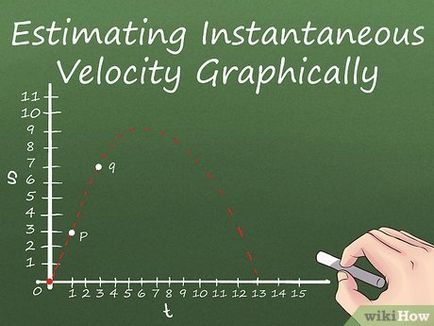
De exemplu, considerăm punctul P (1,3) și Q (4,7) și se calculează viteza instantanee la punctul P.

Găsiți panta segmentului PQ. Înclinarea PQ segmentului este raportul dintre diferența „y“ valori de coordonate ale punctelor P și Q diferenței dintre valorile coordonatelor „x“ puncte P și Q. Cu alte cuvinte, H = (YQ - yP) / (xQ - xP), unde H - panta PQ segment. În exemplul nostru, panta PQ segment este:

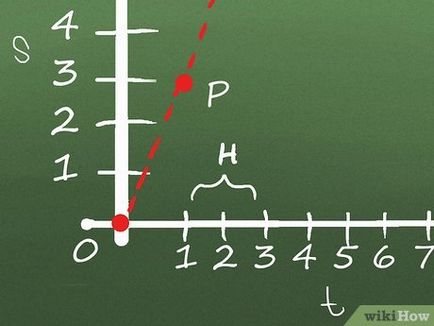
Se repetă procesul de mai multe ori, aducând punctul Q la punctul P. cât este mai scurtă distanța dintre cele două puncte, mai aproape de valoarea pantei obținută pentru panta segmentelor graficului la P. In acest exemplu, calculele sunt efectuate pentru coordonatele punctului Q (2,4.8), (1,5 , 3,95) și (1.25,3.49) (coordonatele punctului P rămân neschimbate):

Mai mici distanța dintre punctele P și Q, mai aproape valoarea H pentru panta graficului, la punctul P. La distanță extrem de mică între punctele P și Q, valoarea H este panta graficului în punctul P. Din moment ce nu se poate măsura sau calcula o extrem de mică distanța dintre două puncte, metoda grafică oferă o estimare a pantei graficului în punctul P.

In exemplul nostru, P Q apropie am obținut următoarele valori: 1.8 N; 1.9 și 1.96. Din moment ce aceste numere au tendința de 2, se poate spune că panta graficului de la punctul P este egal cu 2.
Rețineți că panta la un punct dat este egal cu derivata funcției (care este construit pe acest grafic), în acest punct. Graficul prezinta deplasarea corpului în timp și, după cum sa menționat în secțiunea anterioară, viteza instantanee a corpului este egală cu derivata ecuației de mișcare a corpului. Astfel, se poate afirma că, atunci când t = 2 viteza instantanee este de 2 m / s (aceasta este o valoare estimată).

Partea 3 din 3: Exemple Editare

Se calculează viteza instantanee la t = 4, dacă mișcarea corporală descrisă de ecuația s = 5t 3 - 3t 2 + 2t + 9. Acest exemplu este similar cu sarcina primei secțiuni, cu singura diferență că aici dată ecuația al treilea ordin (și nu al doilea).

În primul rând, vom calcula derivata a acestei ecuații:

s = 5t 3 - 3t 2 + 2t + 9
s = (3) 5t (3 - 1) - (2) 3t (2 - 1) + (1) 2t (1 - 1) + (0) 9t 0 - 1
15t (2) - 6t (1) + 2t (0)
15t (2) - 6t + 2

Acum substitui valoarea derivatului ecuației t = 4:

s = 15t (2) - 6t + 2
15 (4) (2) - 6 (4) + 2
15 (16) - 6 (4) + 2
240 - 24 + 2 = 22 m / s

Estimăm valoarea vitezei instantanee la coordonatele (1,3) pe graficul functiei s = 4t 2 - t. În acest caz, punctul P are coordonatele (1,3) și este necesar să se găsească niște coordonate punctul Q, situată în apropierea punctului P. Apoi calcula H și a găsi valorile estimate ale vitezei instantanee.

În primul rând, descoperim coordonatele Q atunci când t = 2, 1,5, 1,1 și 1,01.

t = 2: s = 4 (2) 2 - (2)
4 (4) - 2 = 16 - 2 = 14, deci Q = (2,14)

t = 1,5: s = 4 (1,5) 2 - (1.5)
4 (2.25) - 9 = 1,5 - 1.5 = 7,5, deci Q = (1.5,7.5)

t = 1,1: s = 4 (1,1) 2 - (1.1)
4 (1.21) - 1,1 = 4.84 - 1,1 = 3,74, deci Q = (1.1,3.74)

t = 1,01: s = 4 (1,01) 2 - (1.01)
4 (1.0201) - 1,01 = 4.0804 - 1.01 = 3.0704, deci Q = (1.01,3.0704)

Deoarece valorile obținute pentru H tind 7, se poate spune că viteza instantanee a corpului la punctul (1,3) este de 7 m / s (valoarea estimată).

Regulamentul

Pentru a găsi accelerația (schimbarea vitezei în timp), utilizați metoda în prima parte pentru a obține derivații funcției de deplasare. Apoi ia derivat mai mult timp derivatului rezultat. Acest lucru vă va da o ecuație pentru accelerația la un moment dat - tot ce trebuie să faceți este să substituie valoarea de timp.
Ecuația care descrie dependența v (deplasarea) x (timp) poate fi foarte simplu, de exemplu: de la = 6x + 3. În acest caz, panta este constantă și nu are nevoie să ia derivatul să-l găsească. Conform teoriei orarelor liniare, panta lor este coeficientul variabilei x, adică, în acest exemplu = 6.
Mutarea ca o distanță, dar are o anumită direcție, ceea ce face o cantitate vector. Mutarea poate fi negativ, în timp ce distanța va fi doar pozitiv.