Cum de a găsi partea unui triunghi isoscel, în cazul dat bazei

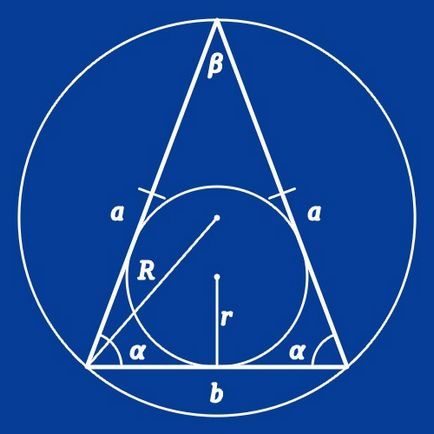
Marcați laturile și unghiurile unui triunghi isoscel. Lăsați baza este b, partea laterală a, unghiurile dintre latura laterală și subunitatea de bază, unghiul subîntins p bază, înălțimea h.

Localizați partea folosind teorema lui Pitagora, care prevede că pătratul ipotenuzei unui triunghi dreptunghic este egal cu suma pătratelor picioarelor - c ^ 2 = a ^ 2 + b ^ 2. Dacă, în plus față de baza unui triunghi isoscel este cunoscut pentru înălțime, atunci este un triunghi isoscel proprietăți este mediana și împarte forma geometrică în două triunghiuri drepte egale.

Substitut în ecuație valorile dorite. Deci, în acest caz, ar fi: a ^ 2 = (b / 2) ^ 2 + h ^ 2. Rezolva ecuația: a = √ (b / 2) ^ 2 + h ^ 2. Cu alte cuvinte, laturile rădăcinii pătrate este extrasă din suma jumătate din bază, pătrat, și înălțimea, care este de asemenea luată în pătrat.

Dacă un triunghi isoscel - dreptunghiular, colțuri, la baza sa egal cu 45 °. Se calculează latura prin teorema sine: a / păcat 45 ° = b / păcat 90 °, unde b - bază, și - partea laterală, păcat de 90 ° este egal cu unitatea. Rezultatul este: a = b * sin 45 ° = b * √2 / 2. Aceasta este, partea laterală a bazei este înmulțită cu rădăcina pătrată a două împărțit la doi.

Utilizați legea sinus și în cazul în care un triunghi isoscel nu este dreptunghiular. Subunitățile de bază și unghi care înconjoară localizați lateral. a = b * sinα / sinβ. Unghiul β folosind proprietățile calculate ale triunghiurilor, care prevede că suma tuturor unghiurilor într-un triunghi este egal cu 180 °: β = 180 ° - 2 * α.

Se aplică teorema cosinusului în conformitate cu care parte a triunghiului este egală cu pătratul sumei pătratelor celorlalte două laturi minus de două ori produsul din partea de date, înmulțită cu cosinusul unghiului dintre ele. În ceea ce privește triunghiul isoscel cu formula de mai sus este după cum urmează: a = b / 2cosα.

În această figură, ca un triunghi dreptunghic sigur că există un raport de aspect clar în raport cu celălalt. Cunoscând doi dintre ei, puteți găsi întotdeauna un al treilea. Modul în care acest lucru poate fi făcut, vei învăța de la instrucțiunile oferite mai jos.

Cuadratura atât piciorul, și apoi adăugați-le împreună a2 + b2. Rezultatul este ipotenuza (baza) în c2 pătrat. În continuare, aveți nevoie doar de a elimina rădăcina în ultima zi, și a găsit ipotenuza. Această metodă este cea mai simplă și ușor de utilizat în practică. Important în procesul de a găsi laturile triunghiului astfel încât - nu uitați să extragă rădăcina pătrată a rezultatelor preliminare, pentru a evita cele mai comune greseli. Formula este derivată prin cele mai renumite din lume, din teorema lui Pitagora, care, în toate sursele este după cum urmează: a2 + b2 = c2.

Împărțiți unul dintre picioarele într-o condiție sine se opune să-l unghi păcat α. În cazul în care o parte cunoscută condiție și sinusurile, această realizare va găsi ipotenuzei cea mai acceptabilă. Formula în acest caz va avea o formă foarte simplă: c = a / păcat α. Fii atent la toate calculele.

Înmulțiți partea a două. Ipotenuză este calculat. Aceasta este, probabil, cea mai de bază metoda de a găsi partea corectă a noi. Dar, din păcate, această metodă se aplică numai într-un singur caz - în cazul în care există o parte care se află vizavi de grade măsură unghi egal cu numărul de treizeci de ani. Dacă este cazul, puteți fi sigur că va fi întotdeauna o exact jumătate din ipotenuzei. Prin urmare, puteți crește doar de două ori și răspunsul gata.

Se împarte o catetă și cosinusul unghiului adiacent la acesta cos a. Această metodă este adecvată numai în cazul dacă știți unul dintre picioare și cosinusul unghiului adiacentă acesteia. Această metodă seamănă cu deja prezentată mai devreme, care este folosit ca piciorul, dar în loc de cosinusul - sinusul unghiului opus. Doar aici formula în acest caz va avea mai multe alte aspect modificat: c = a / cos α. Asta e tot.

Isoscel sau un triunghi echilateral este numit, în care lungimea celor două laturi ale aceleași. Dacă este necesar, calcularea lungimii unei laturi a acestei cifre se poate folosi cunoașterea valorilor unghiurilor în nodurile sale în combinație cu lungimea unei laturi sau raza cercului circumscris. Acești parametri poligon teoreme de sinus, cosinus, și alte câteva raport constant legat.

Pentru a calcula lungimea laterală a triunghiului isoscel (b) lungimea cunoscută a bazei condițiilor (a) și valoarea unghiului adiacent (a) folosind teorema cosinus. Din aceasta rezultă că ar trebui să împartă lungimea laturii cunoscute la dublul cosinusul unghiului condițiilor indicate în: b = a / (2 * cos (α)).

Aceeași teorie se aplică la operația inversă - calcularea lungimii de bază (a) de lungime cunoscută unei laturi (b) și mărimea unghiului (a), între cele două părți. În acest caz, teorema permite obținerea egalității, porțiunea din dreapta conține de două ori produsul din lungimea laturii cunoscute de cosinusul unghiului: a = 2 * b * cos (α).

Dacă lungimile altele decât (b) părți în condiții indicate unghiul valorii ele (β), pentru a calcula lungimea bazei (a) utilizează teorema sine. Din această formulă rezultă, potrivit căreia ar trebui să fie de două ori lungimea laturii înmulțită cu sinusul jumătate dintr-un unghi cunoscut: a = 2 * b * sin (β / 2).

Teorema sinus poate fi utilizată pentru a găsi lungimea laturii (b) a unui triunghi isoscel dacă lungimea cunoscută de bază (a) și mărimea unghiului opuse lui (β). În acest caz, dublu sinusul jumătate forma unghiului și se împarte valoarea rezultată a lungimii bazei: b = a / (2 * sin (β / 2)).

Dacă triunghiul aproximativ isoscel este descris un cerc a cărui rază (R) este cunoscută, pentru calcularea lungimile laturilor trebuie să știe unghiul la unul dintre nodurile figurii. În cazul în care condițiile include informații despre unghiul dintre laturile (p), Calculati lungimea bazei (a) raza de lucru poligon dublarea valorii sinusul unghiului: a = 2 * R * sin (β). Dacă o anumită valoare a unghiului de la baza (α), pentru a găsi lungimea laturii (b), pur și simplu înlocuiți unghiul în această formulă: b = 2 * R * sin (α).