Curbura și raza de curbură a traiectoriei - studopediya

Curbura unei curbe în care - unghiul de rotație la o tangentă la lungimea secțiunii curbe.

Raza de curbură - valoarea reciprocă a curburii:

Raza de curbură a cercului este raza cercului; Raza linie curbura este infinit. Raza de curbură se măsoară în metri.

Punct Normal, a cărui distanță de un punct dat al traiectoriei în direcția concavitatea curbei la distanță, numit centrul de curbură a curbei corespunzătoare unui anumit punct al curbei. Locusul centrelor de forme de curbură linia - curba înfășurătoare original (evolutus (lat) - expandat ;. Voluto - role, rola). Curba evolventă inițială este relativ la înfășurătoare sale (evolventis - dezlegare).

♦ Dacă traiectoria aproximativă a zonei (Fig. 2), arc de cerc, centrul său se află în punctul de intersecție perpendiculare recuperate din mediane coardelor și. Poziția punctului prevăzut Limitarea. atunci când. este centrul de curbură al traiectoriei în punctul M.

Dacă raza R de la rolă la rolă firul de fixare porțiune dreaptă rewind, capătul firului descrie un cerc involuează, și anume corespunzător punctului de la care a început firele final Mosey. Fig. 3, și arată raza cercului evolventă. care corespunde punctului de pornire extrema dreaptă pentru firul este înfășurat invers acelor de ceasornic. Ecuațiile parametrice ale evolventă

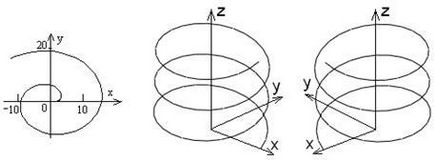
Fig. 3. evolventă unui cerc. spiralele

Când această curbă este aproape de spirala lui Arhimede, a cărui ecuație în coordonate polare.

Dinții roților de cele mai multe unelte de pescuit au profil evolventă, minimizând astfel alunecarea și dinte pentru dinte de fabricație simplificată se treptele de viteză. Profilul bază cuprinde dinți involută ( „scanare“) cercul de bază (cm. „Teoria mașinilor și a mecanismelor“) angajarea roților.

1.1.15. triedru naturale (triedru naturale) - triedru, construit pe axele de tangenta, normal și binormals. vector unitate Binormal este definit ca; atunci. Osculating plan trece prin tangenta și normală. Avionul care conține normal și binormal, numit planul normal, și planul care conține binormal și tangenta - rectificare. triedru natural orientat în spațiu în funcție de forma curbei. Informații despre forma (geometria curbei interioare) poate fi utilizat pentru a investiga o mișcare punct material pe această curbă.

Curba spațială, indiferent de locația în raport cu obiectele din jur pot fi descrise prin definirea la fiecare punct de curbură și torsiune (curba grecescul „kappa“.):

Magnitudinea torsiunii unde - unghiul de rotație al binormal la aria lungimea curbei.

Formulele Serret - Frenet:

Curbura - parametru pozitiv. Torsiunea helix „dreapta“, prezentat în Fig. 3, b este pozitiv. Torsiunea „stânga“ (Figura 3c.) - negativ.

1.1.16. Uniform mișcare accelerată este determinată de starea punctului

; apoi au formulele: