Forced oscilații mecanice 1

Denote - unghiul dintre deplasare și forța motrice.

Substituind (3.3.3), (3.3.4) și (3.3.5) până la (3.3.1):

Fiecare termen în ultima ecuație poate fi reprezentată ca amplitudinea corespunzătoare a vectorilor rotative:

- amplitudine de accelerație; - amplitudinea vitezei; - amplitudinea deplasării; - amplitudinea forței motrice. și

forța vector de amplitudine găsit în regula de adăugare vector:

.

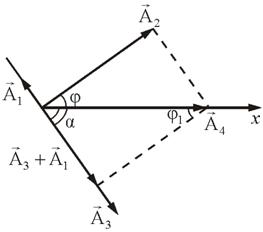
Fig. 3.2 arată că. Găsim amplitudinea A:

.

Astfel, ambele.

La F0 constantă. β m, iar amplitudinea depinde numai de raportul dintre ω pulsația a forței motrice și oscilații neamortizate liber ω0 sistem.

Faza inițială a oscilațiilor forțate pot fi găsite din expresia

Fig. 3.3 arată că forța înainte de offset la un unghi, care este determinat de expresia

.

1) (frecvența forței motrice este zero), atunci

- amplitudinea statică (vibrații nu apar).

2) (fără amortizare). Odată cu creșterea w (dar) crește amplitudine și brusc crește (). Acest fenomen se numește rezonanță. Odată cu creșterea în continuare w () scade de amplitudine din nou (fig. 3.4).

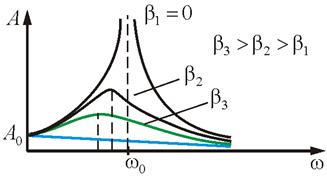
3) Amplitudinea maximă va fi la valoarea minimă a numitorului. Pentru a găsi punctele de inflexiune ia primul derivat al radicand ω (3.3.7) și setați-o egală cu zero:

4ω ≠ 0 și, prin urmare, expresia din paranteze este egală cu zero: