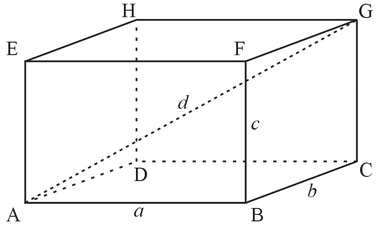
Înălțimea cutiei

Absolut nici o diferenta ce o cutie, înclinat sau drept. Înălțimea lui - este distanța minimă dintre bazele.

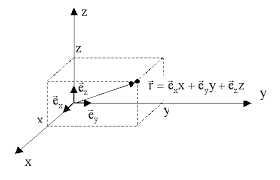
Într-un sistem de coordonate rectangular (cunoscut ca cartezian mai mult), înălțimea paralelipipedului este o proiecție a vectorului razei (paralelipiped diagonală)

pe axa de coordonate (a axe de coordonate). Deoarece partea de sus a casetei coincid cu proeminențele sale (înălțime), este evident că a trebui să găsească înălțimea coordonatele diagonalei - este ușor. Pentru comoditate, este important să se aleagă originea dreapta.

În cazul în care volumul cutiei este cunoscut, cel mai simplu mod de a găsi înălțimea formula de volum este direct proporțională cu volumul și invers proporțional cu suprafața de bază.

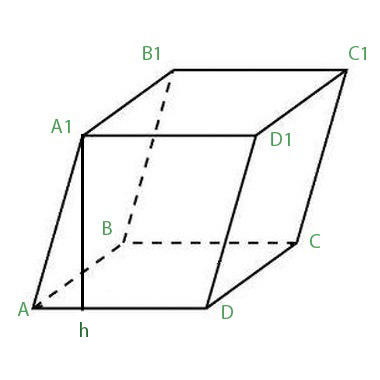
Paralelipipede sunt drepte sau înclinate. Pentru a găsi înălțimea cutiei înclinată să împartă volumul său în zona de bază.

Formula pentru a găsi altitudinea paralelipiped dreptunghic, după cum urmează: h = V / S, unde real V - volumul și S - amprenta cifrele noastre.

Înălțimea paralelipipedului dreapta este chiar mai ușor, deoarece este egală cu lungimea oricărei față laterală perpendiculară pe sol. Acest lucru este ușor de dovedit folosind același forum de stocare h = V / S, care suntem obișnuiți. Știm că, în scopul de a direcționa caseta V = a * b * c, și S = a * b. In consecinta h = a * b * c / a * b = c. Prin urmare: h = c.