numere de conjugat

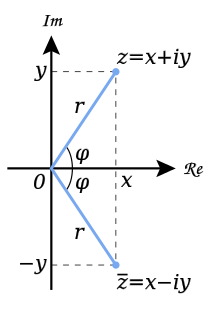
Reprezentarea geometrică a numerelor de conjugat

În cazul în care un număr complex. atunci numărul este denumit conjugat (sau conjugat complex) la (adesea indicat, de asemenea). Pe plan complex numărul conjugat obținut prin imagini în oglindă unul față de altul în raport cu axa reală. Numărul modulului conjugat este identic cu originalul, iar argumentele lor sunt diferite în semn.

Tranziția la numărul de împerechere poate fi considerată ca o operațiune unary; enumera proprietățile sale.

· (Conjugat la imperecherea are originalul).

Produsul și cantitatea de numere complexe conjugate este un număr real:

·

·

·

·

Rezumat :. în cazul în care - un polinom arbitrar, cu coeficienți reali. Din aceasta rezultă că polinomul cu coeficienți reali are fie numai rădăcini reale, sau în cazul în care are rădăcini cu partea imaginară nenul, acestea sunt împărțite într-o pereche de complex conjugat.

Produsul a numerelor complexe conjugate importante în mecanica cuantică nu are nici o semnificație fizică a funcției de undă complexă a sistemului microparticulei care descrie în mod exhaustiv fiind multiplicat cu conjugat său complex dă având fizică densitate de probabilitate semnificația de a găsi o particulă la punctul considerat.

Multiplicarea numărătorul și numitorul fracției complexului când conjugatul complex al numitorul expresiei la numitorul folosit pentru a elimina complexitatea numitorul, care ne permite să-și exprime expresia în forma canonică a unui număr sau funcții complexe.

·

·

semnificație conjugare datorită faptului că acesta este un generator al grupului Galois.

Reprezentarea numerelor complexe