Portalul Educațional Tsu
Pe plan intern, numite astfel de fluctuații care apar într-un sistem oscilatorie sub acțiunea forțelor externe schimbă periodic (am forța motrice suna). Să forța motrice variază în funcție de legea armonică
În compilarea ecuațiile de mișcare necesare pentru a lua în considerare, pe lângă forța motrice, de asemenea, forțele care acționează în sistem sub vibrații, adică forța ,. Quasielastic și forța de tragere. fluctuații Presupunând că destul de mici, vor continua să fie considerată forță proporțională cu rata de rezistență. Apoi, ecuația de mișcare poate fi scrisă astfel:
Împărțind această ecuație prin m și deplasarea membrilor cu x și x pe partea stângă, obținem ecuația neomogenă liniare diferențiale de ordinul doi:
în care: - coeficientul de amortizare, frecvența naturală de oscilație a sistemului.
După cum știm din teoria ecuațiilor diferențiale, soluția generală a ecuației neomogene este suma soluției generale a ecuației omogene corespunzătoare și o soluție particulară a ecuației neomogene. știm deja soluția generală a ecuației omogene [vezi. Funcția (73,10) este soluția generală a ecuației (73,2)]. Ea are forma
Funcția (75,9), în valoare de (75.3) dă soluția generală a ecuației (75.2), care descrie comportamentul sistemului sub oscilații forțate. Termenul (75,3) joacă un rol important numai în faza inițială a procesului, așa-numitele de stabilire a oscilațiilor (Fig. 188)
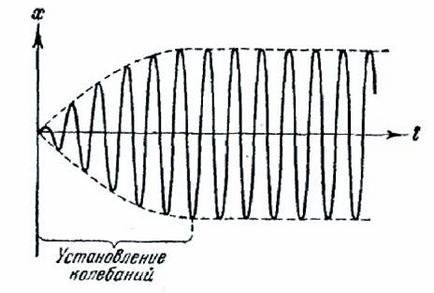
De-a lungul timpului, datorită factorului exponențial rolul termenului (75.3) este tot mai redusă și suficient timp, ea poate fi ignorată, păstrând doar termenul în soluție (75,9).
Astfel, funcția (75.9) descrie vibrațiile de echilibru forțate. Ele reprezintă oscilații armonice cu o frecvență egală cu forța motrice. Amplitudine (75,7) proporțională cu amplitudinea vibrațiilor forțate ale forței motrice. Pentru acest sistem oscilatorie (și definit), amplitudinea depinde de frecvența forței motrice. vibrațiile lag fazei de o forță forțat îndemnând, în care valoarea de lag de asemenea, depinde de frecvența forței motrice [vezi. (75,8)].
Dependența de amplitudinea oscilațiilor forțate de frecvența de conducere cauzele de forță „, care, în unele specifice pentru o amplitudine sistem de frecvență de oscilație dat atinge o valoare maximă, sistemul vibrațional este in mod special receptiv la acțiunea forței motrice la această frecvență. Acest fenomen se numește rezonanță, și frecvența corespunzătoare - frecvența de rezonanță.
Pentru a determina frecvența de rezonanță. necesitatea de a găsi maximul funcției (75,7) sau, echivalent, minimul expresiei sub rădăcina pătrată la numitor. Diferențierea această expresie cu respect și egalează cu zero, obținem condiția care determină:
Din (75.12) rezultă că, în absența rezistenței mediului la o amplitudine de rezonanță ar deveni infinit. Conform (75,11), frecvența de rezonanță, în aceleași condiții (at) coincide cu frecvența naturală de oscilație a sistemului.
Dependența amplitudinii oscilațiilor forțate ale frecvenței forța motrice (sau, camoe de frecvență echivalent oscilație) este prezentată grafic în Fig, 189. curbe separate pe grafic corespund diferitelor valori ale unui parametru. Conform (75.11) și (75.12) decât mai puțin. cele de mai sus și la dreapta acestei curbe este maximă. La o atenuare foarte mare (astfel încât) expresia pentru frecvența de rezonanță devine imaginar. Acest lucru înseamnă că, în aceste condiții de rezonanță nu au fost observate - cu creșterea frecvenței amplitudinea oscilațiilor forțate este în scădere uniform (vezi curba de jos în Figura 189 ..). prezentat în
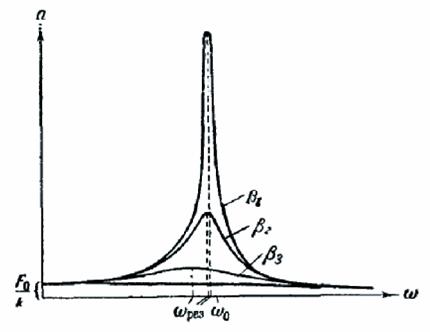
Fig. 189 set de grafice de funcții (75.7), care corespund diferitelor valori ale parametrului. Se numește curbe de rezonanță.
În ceea ce privește curbele de rezonanță pot face următoarele observații. Tinde la zero, toate curbele vin la aceeași non-zero, valoarea limită egală. t. e. F 0 / k. Acesta este un decalaj față de poziția de echilibru, care primește sistemul sub o forță constantă de magnitudine F 0. Într-un efort la infinit, toate curbele se apropie asimptotic de zero, deoarece frecvența ridicată a puterii se schimbă atât de repede de direcție, sistemul nu reușește să schimbe în mod evident de la poziția de echilibru. În cele din urmă, rețineți că cea mai mică. c mai puternic variază în apropierea frecvenței de rezonanță a amplitudinii, a „clară“ se obține max.
Din formula (75.12) Rezultă că pentru atenuare scăzută (m. E. La), amplitudinea la rezonanță este aproximativ egală cu
Se împarte deplasament această expresie xq din poziția de echilibru sub acțiunea unei forțe constante F 0. egal, așa cum am descoperit. Rezultatul:
[V. formula (73.13)]. Astfel, factorul de calitate Q indică de câte ori amplitudinea la punctul de rezonanță depășește sistemul de compensare din poziția sa de echilibru sub acțiunea forței constante de aceeași magnitudine ca și amplitudinea forței motrice (acest lucru este valabil numai pentru o atenuare mică).
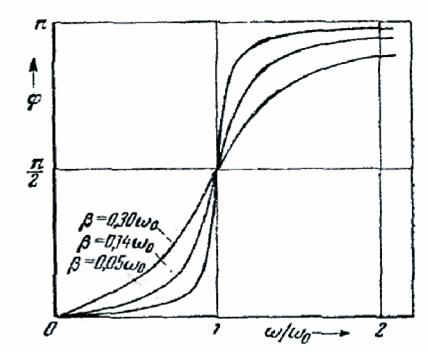
După cum se poate observa din Fig. 187, oscilație forțată se situează forța motrice cu valoarea de lag se află în intervalul de la 0 la. Dependența de la valori diferite este prezentată grafic în fig. 190. Frecvența corespunde. Rezonant frecvență mai mică decât naturale [vezi. (75.11)]. Prin urmare, în momentul de rezonanță. Atunci când slab de amortizare. Valoarea 0 la rezonanță, poate fi considerat egal.
Cu fenomenul de rezonanță pentru a fi socotit cu în proiectarea de mașini și tot felul de construcții. Frecvența de vibrație a acestor dispozitive, în orice caz, nu ar trebui să fie aproape de frecvența de posibile influențe externe. De exemplu, frecvența naturală de vibrație a corpului navei sau aripa aeronavei trebuie să fie foarte diferită de frecvența de oscilație, care poate fi excitat prin rotirea elicei sau elicelor. În caz contrar, vibrațiile apar ceea ce poate provoca un dezastru. Există cazuri în care sunt afectate de poduri atunci când trece prin ele marș coloane de soldați. Acest lucru sa datorat faptului că frecvența naturală de oscilație a podului este aproape de frecvența cu care coloana în trepte.
Bmeste cu fenomenul de rezonanță este adesea foarte util, mai ales în acustică, radio și așa mai departe. D.