Ecuația liniei ce trece prin punctele date

Dacă dat puncte specifice, de exemplu, A (4; 10) și B (1 și 2), atunci ecuația poate fi găsită prin rezolvarea sistemului de ecuații.

În cazul în care A și B au un alt prim coordonate (abscisă), linia dreaptă pe care se află punctele nu este paralelă cu axa y și este descrisă de ecuația y = kx + b. Mai sus sistemul de ecuații și de a rezolva aceasta. De exemplu:

| 10 = 4k + b,
| 2 = k + b.

b = 2 - k
10 = 4k + 2 - k
8 = 3k
k = 8/3

și ecuația liniei este dată.

Cu toate acestea, putem obține o formă generală a unei ecuații liniare exprimată prin coordonate A (x1, y1) și B (x2; y2), dacă x1 ≠ x2.

b = y2 - KX2
y1 = KX1 + y2 - KX2
y1 - y2 = KX1 - KX2
y1 - y2 = k (x1 - x2)

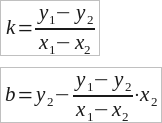
Cunoașterea b și k. puteți obține acum ecuația în forma generală:

Transformarea algebric, această ecuație poate fi redusă la o formă mai simplă:

.