Metoda noduri în problema b5
Există o formulă minunat care ne permite să ia în considerare aria unui poligon pe grila cu aproape nici o eroare. Nu este nici o formulă, iar prezenta teorema. La prima vedere, poate părea descurajantă. Dar este de ajuns pentru a rezolva o serie de probleme - și veți vedea modul în care această caracteristică se răcească. Deci, mergeți mai departe!
Pentru a începe, vom introduce o nouă definiție:
Nod de coordonate stive - este orice punct care se află la intersecția liniilor verticale și orizontale ale grilei.
În prima imagine, în general, nodurile nu sunt marcate. 4 sunt desemnate la al doilea nod. În cele din urmă, toate cele 16 unități sunt marcate în a treia imagine.
Cum acest lucru se referă la B5 problema? Faptul că vârfurile poligonului în astfel de probleme sunt întotdeauna în nodurile ochiurilor de plasă. În consecință, ei lucrează următoarea teoremă:
Teorema. Luați în considerare grila de poligon a cărui noduri se află la nodurile rețelei. Apoi, zona poligonului este egală cu:
unde n - numărul de noduri într-un anumit poligon, k - numărul de noduri care se află la limita (nodurile de frontieră).
Ca un exemplu, ia în considerare un triunghi regulat pe grila și să încerce să rețineți nodurile interne și de frontieră.
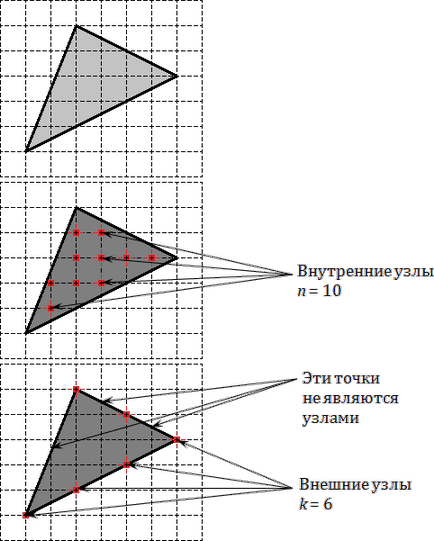
Prima imagine este dat un triunghi regulat. Pe al doilea marcat componentele sale interne, al căror număr este egal cu n = 10. La nodurile treia imagine marcate situată la granița, există doar k = 6.
Poate că mulți cititori nu înțeleg cum de a contoriza numărul de n și k. Începeți cu nodurile interne. Este totul clar: vopsea creion triunghi și a vedea cât de multe site-uri au venit sub umbrire.
Cu un pic de noduri la limită mai complicate. Limita poligonului - o polilinie închisă. care traversează grila în multe locuri. Cel mai simplu mod de a observa orice punct „de pornire“, și apoi trece restul.
nodurile de delimitare sunt doar acele puncte pe linia întreruptă, în cazul în care trei linii se intersectează în același timp.
- De fapt, o linie întreruptă;
- Linia orizontală a grilei;
- Linia verticală.
Să vedem cum funcționează în aceste sarcini.
Sarcină. Găsiți o zonă de triunghi, în cazul în care dimensiunea celulei este de 1 x 1 cm:
Pentru a începe cu noduri care se află în interiorul triunghiului, precum și la frontiera sa:
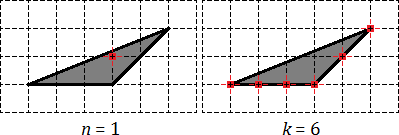
Se pare că numai un singur nod intern: n = 1. noduri la limită - cât mai multe de șase, trei coincid cu vârfurile triunghiului. și trei sunt pe părțile laterale. Total k = 6.
Acum, ia în considerare zona folosind formula:
Asta este! Problema este rezolvată.
Sarcină. Găsiți zona patrulaterul prezentată în graficul de hârtie cu dimensiunea celulei de 1 cm cu 1 cm. Raspuns pentru a da centimetri pătrați.

Din nou, observăm nodurile interne și de frontieră. nodurile interne ale tuturor n = 2. noduri limită: k = 7, din care 4 sunt vârfurile patrulaterului. și 3 mai sunt pe părțile laterale.
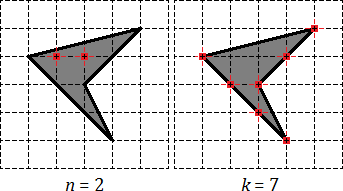
Rămâne să înlocuiască numerele n și k în formula pentru zona:
Notă importantă privind zonele
Dar formula - asta nu e tot. Să rescrie formula, aducand termeni privind dreptul la un numitor comun. obținem:
Numerele n și k - este numărul de noduri, ele sunt întotdeauna numere întregi. Deci, de asemenea, un întreg numărător. Am împărți cu 2, ceea ce implică un fapt important:
Zona este întotdeauna exprimată de un număr întreg sau fracțiune. Iar la sfârșitul fracțiunii este întotdeauna „cinci zecimi“: 10,5; 17,5, etc.
Astfel, în zona B5 problemă este întotdeauna exprimată de un număr întreg sau o fracțiune din forma *** 5. În cazul în care răspunsul este diferit, înseamnă că undeva o greșeală. Păstrați acest lucru în minte atunci când ia examenul real de la matematică!
- Pregătirea gratuită pentru examenul de 7 lecții simple, dar foarte util + teme pentru acasă
