oscilații forțate și rezonanță
În cazul în care un corp cu masa m sunt forța elastică Fy = -kX, forța de frecare
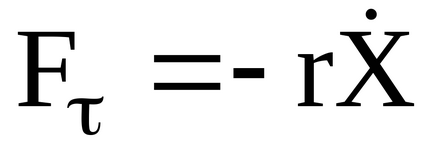
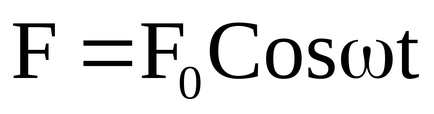
unde
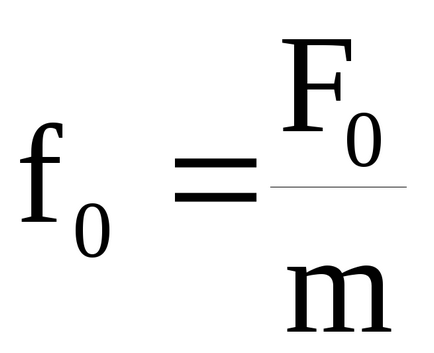
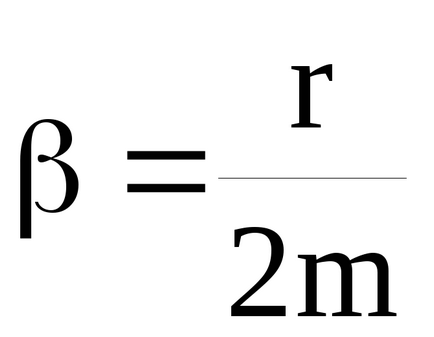
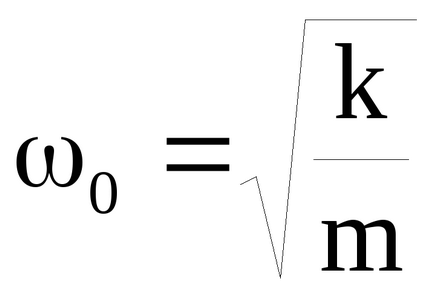
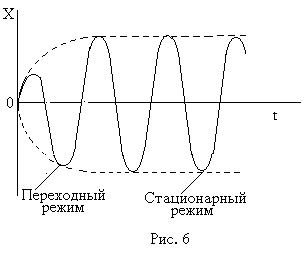
încă plin de energie conferit de forță externă nu va fi pe deplin petrecut în depășirea frecării, care este proporțională cu viteza. De aceea, echilibrul este stabilit în care suma de energie cinetică și potențială este constantă. Această condiție caracterizează starea de echilibru a sistemului.
În această stare, mișcarea corpului va fi armonic cu o frecvență egală cu frecvența de excitație externă, ci din cauza inerției oscilațiilor sale vor fi transferate în faza în raport cu valoarea instantanee a forței externe periodice:

Spre deosebire de oscilație liberă amplitudine A și faza forțată oscilație
nu depind de condițiile inițiale de mișcare, și va fi determinată numai de proprietățile sistemului oscilant, amplitudinea și frecvența forței motrice:
Se poate observa că amplitudinea și defazajul depinde de frecvența forței motrice (Fig.7 și 8).
O trăsătură caracteristică este prezența de rezonanță oscilație forțată. Aspectul de creștere bruscă a amplitudinii de oscilație forțată atunci când frecvența forței motrice la frecvența naturală a corpului liber oscilațiilor neamortizate ω0 se numește rezonanță mecanică. Amplitudinea oscilației corpului la frecvența de rezonanță
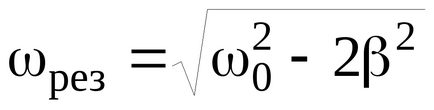
În ceea ce privește curba de rezonanță (vezi. Fig. 7), vom face următoarele observații. Dacă ω → 0, atunci toate curbele (a se vedea. De asemenea, (35)), vin la aceeași nenulă, valoarea limită
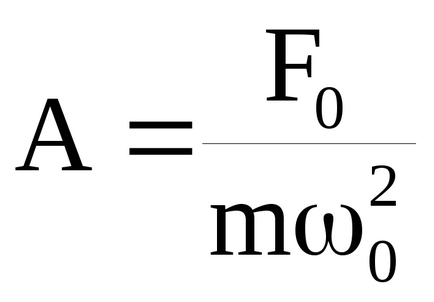
Cu condiția atenuare mică (β 2 << ω0 2) rezonanță amplitudine (cm. (37))
În conformitate cu această condiție, să ia de rezonanță compensa relația cu deformarea statică.
,
care arată că creșterea relativă a amplitudinii de oscilație la rezonanță este determinată de calitatea sistemului de vibrație. Aici, factorul de calitate este, în esență, un câștig de răspuns
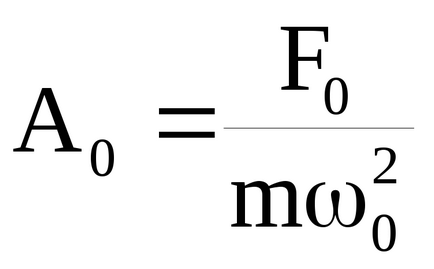
Această situație provoacă un fenomen de rezonanță de o mare importanță în fizică și inginerie. Folositi-l dacă doresc pentru a spori vibrațiile, de exemplu, în acustică - pentru a îmbunătăți sunetul instrumentelor muzicale, radio, - pentru a selecta semnalul dorit dintr-o varietate de alte frecvențe diferite. În cazul în care mozhetprivesti rezonanță cresc indezirabil sistem de oscilație utilizat cu factor Q scăzut.
Sursa unei forțe externe periodice poate fi al doilea sistem vibrator, elastic legat cu primul. Ambele sisteme oscilante pot acționa pe unul pe altul. Astfel, de exemplu, cazul a două pendule cuplate (Fig. 9).
Sistemul poate efectua atât în fază (Fig. 9b) și (9c Fig.) Fluctuații anti-fază. Aceste vibrații sunt numite de tip normal sau modul normal de oscilație și se caracterizează prin propria lor frecvență normală. Când mod comun prejudecată a pendule oscilații la toate punctele de timp X1 = X2. ω1 și frecvența este aceeași ca frecvența unui singur pendul
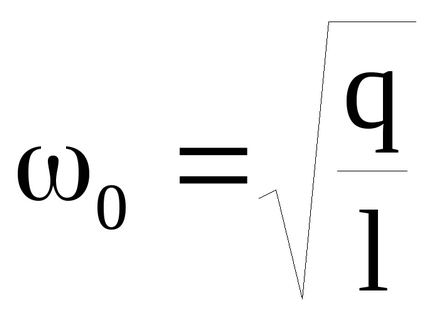
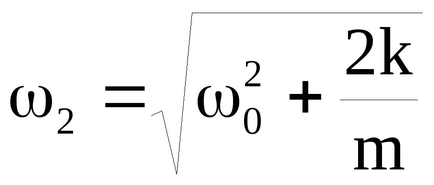
(. Figura 9a) Orice stare a sistemelor noastre conexe, inclusiv deplasarea inițială X, poate fi reprezentat ca o superpoziție a două moduri normale:
Dacă sistemul de plumb în mișcare de X1 starea inițială = 0,
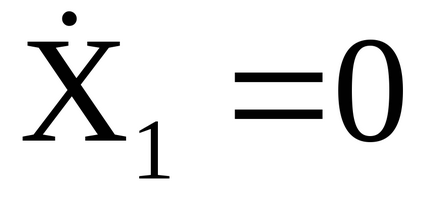
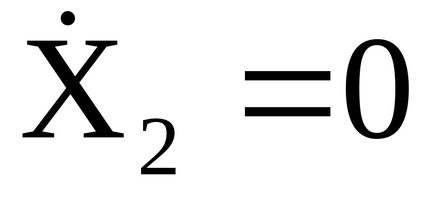
deplasarea pendulului sunt descrise de expresiile:
,
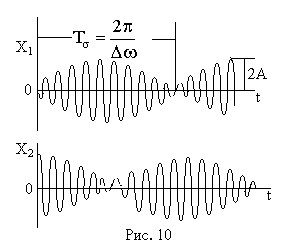
Pendulum frecvență de oscilație egală cu frecvența medie a celor două moduri normale
și amplitudinea acestora variază ca sinusul conului sau cu o frecvență mai mică egală cu jumătate din modurile normale de frecvență diferență
O schimbare lentă în amplitudine cu o frecvență egală cu jumătate din modurile normale ale diferenței de frecvență, numit „bate“ ale celor două frecvențe de oscilație cu aproape identice. Frecvența „bate“ egal cu -ω2 frecvență diferența ω1, (și nu jumătate din diferența), deoarece 2A amplitudinii maximă atinsă de două ori în cursul unei perioade corespunzătoare frecvenței
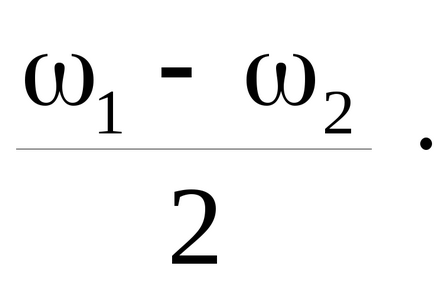
Din această perioadă este egală cu ritmul
Când bate între energia pendulul este schimbată. Cu toate acestea, un schimb de energie complet este posibilă numai atunci când cele două mase sunt identice și raportul (ω1 + ω2 / ω1 -ω2) este un număr întreg. Este necesar să menționăm un punct important: deși pendulele individuale pot face schimb de energie, schimbul de energie între modurile normale disponibile.
Prezența unor astfel de sisteme oscilante care interacționează unele cu altele și capabil să comunice unul cu altul energia lor, constituie baza mișcării valurilor.
corp material oscilând plasat într-un mediu elastic, și antrenând aduce în circulație a particulelor adiacente oscilatorii în mediu. Datorită prezenței legăturilor elastice între particulele cu oscilații caracteristice propaga pentru viteza fluidului peste mediu.
Procesul de propagare a undei în medii elastice numit val. Există două tipuri principale de valuri: longitudinală și transversală. Undele longitudinale ale particulelor de dimensiune medie vibra de-a lungul direcției de propagare a undei, și transversal - perpendicular pe direcția de propagare a undei. Nu este în nici un mediu elastic se poate propaga o unda transversala. val elastic transvers este posibilă numai în medii în care există elastic deformarea de forfecare. De exemplu, în gaze și lichide se aplică numai undelor longitudinale elastice (sunet).
Locul geometric al punctelor de mediu și care la acest punct a atins timpul de fluctuație se numește front de undă. Partea din față val al spațiului separă deja implicat într-un proces de val, zona în care nu a avut loc oscilație. În funcție de forma de undă frontală distinge plat, sferică, cilindrică, etc.
Ecuația unui răsadurile de unde plane într-un mediu omogen lossless are forma
unde ξ (x, t) - deplasarea particulelor mediului cu coordonata X din poziția de echilibru la momentul t, A - amplitudine,
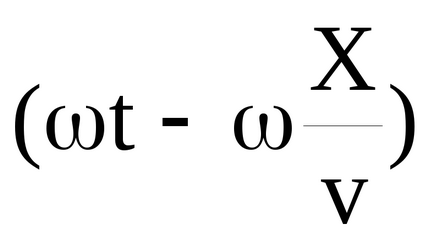
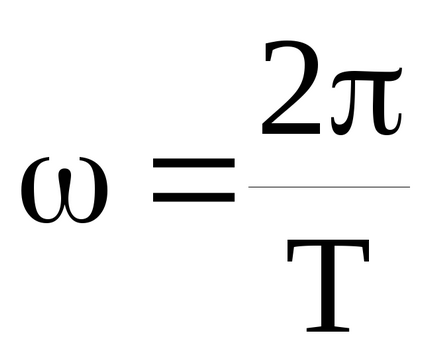
Lungimea de undă λ este distanța dintre punctele, oscilante cu diferența de fază de 2π, cu alte cuvinte, lungimea de undă se numește traseul parcurs de către orice fază de undă într-o perioadă de oscilație:
viteza de fază, adică Viteza de propagare a acestei faze:
Numărul de undă - numărul de lungimi de undă de montare în lungime 2tt unități:
k = ω / v = 2π / λ. (45)
Substituind această notație în (42), ecuatia unui plan care rulează undă monocromatică poate fi reprezentat ca
Rețineți că ecuația de undă (46) detectează o periodicitate dublă în coordonate și timpul. Într-adevăr, fazele oscilațiilor sunt aceleași ca coordonatei pentru λ și
timp pentru schimbarea T (perioada). Prin urmare, grafic nu poate val la avionul. timpul t Adesea fix și diagrama reprezintă dependența deplasării coordonate X ξ, adică distribuția instantanee a particulelor medii de deplasare de-a lungul direcției de propagare a undei (Figura 11). Diferența de fază Δφ dots medie oscilațiilor depinde de distanța X2 = A H - X1 între aceste puncte
Dacă unda se deplasează opusă direcției X, ecuația undelor înapoi scrise sub forma:
ξ (x, t) = ASOS (ωt + Kx). (48)
Standing valuri - este rezultatul unui tip special de interferență val. Acestea sunt formate prin suprapunerea două valuri care călătoresc se propagă în direcții opuse cu frecvențe și amplitudini identice.
Ecuațiile două unde plane se propagă de-a lungul axei X, în direcții opuse, au forma:
Adăugarea acestor ecuații utilizând cantitatea de formula cosinusului și având în vedere că k = 2π / λ, obținem ecuația unui undă staționară
cos Modifier ωt arată că în mediu apare puncte de oscilație aceeași frecvență cu ω amplitudine
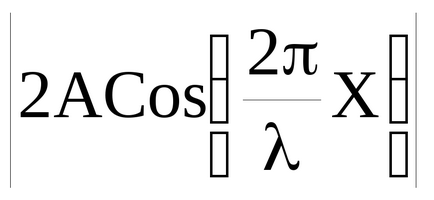
amplitudinea de oscilație atinge o valoare maximă egală cu 2A. Aceste puncte sunt numite ventrele. Din expresia (51) putem găsi coordonatele ventrele:
La punctele unde
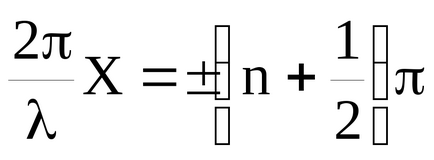
amplitudinea vibrației devine zero. Aceste puncte sunt numite noduri. Coordonatele nodurilor
P
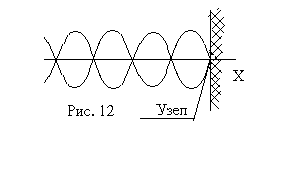
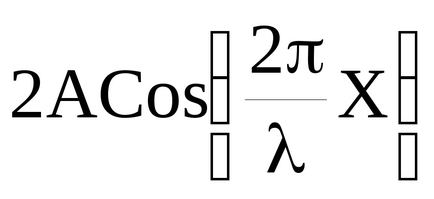
nodurile de distribuție și ventrele în valul în picioare depinde de condițiile existente la interfața dintre două medii, dintre care se produce reflexia. În cazul în care val de reflecție are loc dintr-un mediu mai dens, apoi faza de oscilație la locul undei de reflexie este inversată sau, să zicem, o jumătate de val este pierdut. Prin urmare, ca urmare a adăugării de oscilații în direcții opuse decalate la limita este zero, adică asamblare are loc (fig. 12).

În unda staționară au o deplasare de fază, fără propagare a undei, nu există nici un transfer de energie, care reprezintă numele acestui tip de valuri.