Soluție inegalitățile logaritmice

Soluție inegalitățile logaritmice

Soluție inegalitățile logaritmice are multe în comun cu o decizie orientativă a inegalităților:

a) Pe parcursul tranziției de la logaritmică la exprimare sub logaritm, vom compara, de asemenea, baza logaritmul unității;

b) Dacă vom rezolva inegalitatea logaritmica folosind variabile de substituție, trebuie să decidă dacă să înlocuiască, până când inegalitatea elementară.

Cu toate acestea, există o diferență importantă: deoarece funcția logaritmică are un domeniu limitat, în tranziția de la logaritmică la exprimare sub logaritmul, este necesar să se ia în considerare intervalul de valori admise.

Dacă rezolvarea ecuațiilor logaritmice puteți găsi rădăcinile ecuației, și apoi face o verificare de fond, apoi în rezolvarea inegalităților logaritmice acest număr nu trece: atunci când trecerea de la logaritmi la exprimare în logaritm trebuie să fie înregistrate DHS inegalitate.

Deci Cea mai simplă Inegalitatea logaritmică are forma:

V, unde V - unul dintre semnele de inegalitate: <,>, Sau ≤ ≥.

Dacă logaritmul bazei este mai mare decât unu (), apoi merge la logaritmii expresiei sub semnul logaritm, un semn de inegalitate persistă. și inegalitate

Dacă logaritmul bază este mai mare decât zero și mai puțin de o (), apoi merge la logaritmii expresiei sub semnul logaritm, un semn de inegalitate este inversată. și inegalitate

Luați în considerare exemple de soluții de inegalități logaritmice.

1. Rezolva inegalitatea:

Ca bază logaritmilor pe ambele părți ale inegalității este mai mică de 1, trecerea la expresia sub semnul logaritm, un semn de inegalitate este inversată. Expresia sub logaritmul trebuie să fie strict mai mare decât zero. Ne întoarcem acum la sistem:

Vă rugăm să rețineți: Subliniem faptul că mai mult de zero trebuie să fie cea mai mică dintre expresiile care sunt sub semnul logaritm. În acest caz, o expresie mai mare va fi automat mai mare decât zero.

Noi rezolva sistemul de inegalități:

Rădăcinile polinomului pătratic :,

2. Rezolva inegalitatea:

Vedem că la baza logaritmilor sunt puteri ale lui 2, astfel încât să putem aduce logaritmii în aceeași bază. Facem acest lucru folosind proprietățile logaritmilor:

Se transferă logaritmul unui coeficient negativ de partea stanga a dreapta (ca multiplica mai ușor decât diviza).

Deoarece inegalitatea logaritmii prezent cu aceeași bază și în primul grad, putem reprezenta ambele părți ale inegalității ca logaritmul în baza 2:

Acum putem trece la logaritmii expresiei sub semnul logaritm. Baza este mai mare de 1, astfel încât semnul inegalității persistă. Nu uita despre DHS:

3. Rezolva inegalitatea:

În această inegalitate logaritm ea stă în pătrat, deci este o inegalitate logaritmică vom decide schimbarea de variabile.

În primul rând vom da logaritmii în aceeași bază:

Introducem schimbarea de variabile:

.

Obținem o inegalitate pătratică:

Scriem această dublă inegalitate ca un sistem:

Abia acum, când avem un sistem de inegalități simple, cu respect, ne putem întoarce la variabila originală.

Să ne întoarcem la varazheniyam stând sub semnul logaritm:

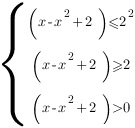
Ultima inegalitate a sistemului - este DHS inegalitatea. Rețineți că este îndeplinită în cazul în care al doilea inegalitatea, astfel încât nu este nevoie să fie abordate.

Primul sistem de inegalitate este transformată într-

Discriminant al acestui polinom pătratic este negativ, senior rezistoare, deci inegalitatea este adevărată pentru orice valori reale.

A doua inegalitate este convertit în forma de aici