inegalitate logaritmică

Deoarece baza logaritmului mai mare de 1, atunci semnul inegalității persistă:

Având în vedere că baza logaritmului este mai mică de 1, schimbarea semn inegalitate:

Traversarea decizia și DHS, avem:

Noi rezolva metoda de intervale. Rădăcina numărătorul -. numitor rădăcină - aceasta este întotdeauna un punct șters, rădăcina numărătorul - se elimină, de asemenea, puncte, ca un semn de stricte. Astfel.

Vom proceda pentru a compara expresiile logaritm, semnul este păstrată: baza este mai mare de 1:

Rădăcina numărătorul -. numitor rădăcină - acest punct înțepat întotdeauna rădăcina numărătorul - la fața locului umbrită, acesta va intra în decizie, ca un semn de inegalitate nu este strictă. Astfel.

În impunerea unor soluții privind DHS obține:

Soluția acestui sistem -

Ca un semn de lax inegalitate, atunci punctele sunt incluse în soluția: acestea ar trebui să reprezinte hașurate în figură. Inegalitatea Soluție :.

Impunerea o soluție pe intervalul de valori admise, obținem:

Soluția acestui sistem -

Punctul 1 este înțepat - este rădăcina numitor, punctul 2 - rădăcina chiar multiplicitate, și să ne amintim că, la aceste puncte ale intervalului semnului nu se schimba! Prin urmare, soluția va arăta astfel:

Acest lucru este pe deplin în conformitate cu DHS, astfel încât răspunsul astfel va:

decizie inegalitatea făcută prin metoda de raționalizare:

Descompune in factori:

Menționăm punctele primite pe axa de coordonate:

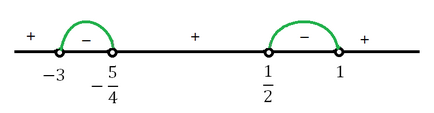
Punerea în practică a deciziei privind DHS, avem: